Já vimos em artigos anteriores medidas de tendência central e de dispersão. Neste artigo vamos falar sobre covariância.
Vamos começar do básico, afinal o que é covariância?
Covariância é um cálculo estatístico que serve para ajudá-lo a entender a relação que dois grupos de dados tem um com o outro.
Como exemplo podemos imaginar a seguinte situação:
Existem dois antropólogos estudando o peso e altura da população em determinada cidade, nesse caso o peso e altura de cada pessoa poderão ser representados por um par de dados (X,Y) valores os quais podem ser utilizados na fórmula padrão da covariância para calculá-la.
Primeiro passo
Primeiro deve-se entender a fórmula padrão da variância. Veja abaixo:
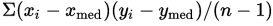
- ?: Sigma. Esta é a letra sigma que representa a somatória dos itens que a seguem em todas as posições de um conjunto;
- xi: Aqui o i representa um índice. Ele está indicando que você está utilizando o valor de x na posição i;
- Xmed: Representa o valor médio do valor de x em todas as posições. Ele também pode ser escrito como um x com uma barra em cima do x sendo chamado de x barra;
- Yi: A mesma coisa que o Xi. Só que ao invés de representar o x na posição i representa o y nessa posição;
- Ymed: Representa o valor médio do valor de y em todas as posições ele também pode ser escrito como um y com uma barra em cima do x sendo chamado de y barra;
- N: Essa variável representa a quantidade de itens em um conjunto de dados;
Segundo passo
Depois de entender a fórmula padrão é preciso coletar todos os dados. É ideal que se tenha a tabela com no mínimo 5 colunas.
Na coluna X você coloca os valores dos pontos de dados em x.
Coluna Y aqui você coloca os valores dos pontos de dados em y. Aqui você deve tomar muito cuidado para botar os valores de y da mesma posição do valor x que está ao lado. Por exemplo, o primeiro valor de y deve ser colocado ao lado do primeiro valor de x.
Coluna Xi-Xmed. No início essa coluna ficará em branco porque ela só será preenchida depois de calcularmos a média dos pontos de x.
A coluna Yi-Ymed é outra coluna que ficará em branco no início sendo posteriormente preenchida depois de calcularmos a média dos pontos de y.
E por fim a coluna produto. Na medida em que você avançar na resolução você deverá ir preenchendo ela. Porém, de início ficará em branco.
Terceiro passo
Agora é necessário que você calcule a média dos pontos de x. Por exemplo, o conjunto 5, 15, 6 e 11. Para calcular a média entre eles some todos e divida por 4 que dará 37/4. O resultado será 9,25. Esse valor será usado como Xmed no futuro.
Quarto passo
Calcule agora a média dos pontos de y do mesmo exemplo de 4 itens. Temos os valores 7, 21, 14, 3.
Para calcular o ymed os somamos e dividimos por 4 o que resultará em 45/4=11,25. Este valor será utilizado como Ymed no futuro.
Quinto passo
Calcule agora os valores de Xi-Xmed.
Finalmente na terceira coluna você precisará calcular a diferença entre cada número de x e o Xmed. Para saber se o resultado é positivo é bem simples. Se estiver acima da média é positivo e se tiver abaixo é negativo. É importante ficar atento aos sinais negativos.
Deves repetir os dados para todos os pontos resultando no seguinte conjunto -4,25 , 5,75 , -3,25 , 1,75.
Sexto passo
Calcule os valores de Yi-Ymed. Você fará o mesmo que com Xi-Xmed. A diferença é que com os valores de y (também deve ficar atento aos valores negativos).
Nesse caso a coluna ficara assim:
-4,25 , 9,75 , 3,75 , –8,25
Sétimo passo
Sim finalmente preencheremos a ultima coluna.
Para isso basta multiplicar os valores de Xi-Xmed por Yi-Ymed. Deve ser feito esse processo em cada linha.
Na primeira linha os valores são -4,25 e -4,25 (deu igual por coincidencia) o que resultara em 18,0625.
Após multiplicar todos você terá o seguinte conjunto 18,0625 , 56,0625 , -12,1875 e -14,4375.
Oitavo passo
Calcular a soma dos valores da última coluna e após calcular todos os valores até aqui deve soma-los.
A soma nesse caso será de 47,5 você deve escrever esse valor no espaço da base da coluna esse valor representará o valor do numerador na fórmula padrão de covariância.
Nono passo
Calcule o denominador da fórmula de covariância.
É bem fácil, basta diminuir 1 do número total de itens na última tabela que é 4 4-1=3. Logo o denominador é igual a 3.
Décimo passo
Agora basta dividir o numerador pelo denominador que fica igual a 47,5/3 que dá igual a 15,83.
E pronto você calculou a covariança!
Espero ter lhe ajudado a esclarecer todas as dúvidas sobre covariança. Quaisquer outras dúvidas, fique a vontade para deixar nos comentários abaixo.
Comentários
Olá. Minha dúvida é como interpretar o resultado. O que 15,83 significa nessa análise de amostra da população? Que há relação entre os dados?
Oi Juliana, tudo bem? A covariância serve para medir a relação linear entre duas variáveis. ;) Visite meu canal no YouTube! Adquira nosso curso completo da para as provas da ANBIMA. Curta nossa página no facebook e não esqueça de compartilhar nosso conteúdo para que possamos continuar com a educação financeira gratuita. Um abraço, Kléber Stumpf