Intervalo de confiança em uma distribuição normal

Olá caro leitor! Em artigos anteriores já falamos sobre a distribuição normal e diversos conteúdos da CPA 20 mas não explicamos devidamente sobre como calcular o intervalo de confiança em uma distribuição normal e nem o que ele.

Então me acompanhe no final dessa jornada matemática sobre estatística e tire suas dúvidas.

O que é um intervalo de confiança?

O intervalo de confiança é um indicador de precisão e estabilidade de uma medida. Através desta medida é possível ver o quão perto a sua medição estará de sua estimativa original repetindo o processo. Então como calcula-lo?

Primeiramente anote o evento que você gostaria de testar, por exemplo, digamos que você está testando o peso médio de um estudante da universidade XYZ do gênero masculino é de 80kg.

Nesse caso você testará a precisão com que é possível prever  o peso dos alunos do sexo masculino da universidade XYZ dentro de um intervalo de confiança.

Depois disso você deve selecionar uma amostra da população escolhida neste exemplo, suponhamos que sejam 1.000 estudantes do sexo masculino. 

No próximo passo você deve calcular a média e o desvio padrão da amostra e escolher uma destas para utilizar como seu parâmetro populacional. Um parâmetro populacional é um valor que representa uma característica determinada da população.

Para calcular a média basta somar todos os dados (nesse caso o peso de todos da amostra) e dividir pelo número de dados.

Digamos que o resultado seja 84kg e para calcular o desvio padrão encontre a média e a variância (que é a média das diferenças da média quadrada). Quando encontrar esse número, basta extrair a raiz que nesse caso dará 13,60kg .

Depois de tudo isso você deve escolher o intervalo de confiança desejado que pode ser 90%, 95% ou 99%. Digamos que você escolheu 95%. Depois temos que calcular a margem de erro que é possível obter através da seguinte fórmula:

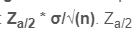
Esta fórmula resulta no coeficiente da confiança em que nível de confiança = desvio padrão. E “n” o tamanho da amostra. Esta outra maneira de dizer que você deve multiplicar o valor crítico pelo erro padrão.

Para calcular o valor crítico Za/2 deve-se ver o nível de confiança que aqui é de 95%, ou seja, 0,95. Agora divide-se por dois para obter 0,475. Após isso deve-se consultar a tabela z  para encontrar o valor correspondente a 0,475 e verá que o valor mais próximo é de 1,96 cruzando a linha 1,9 com a coluna 0,06.

Após isso você deve pegar o valor do erro padrão e do desvio padrão 13,6 e dividir pela raiz quadrada do tamanho da amostra 1.000 que dará 13,6/31,6, ou seja, 0,43. Feito isso multiplique 1,96 por 0,43 para obter sua margem de erro que será de 0,8428.

Agora só falta você indicar o intervalo de confiança. Para isso basta pegar a média de 84 e escrever +- ao lado (o mais em cima do menos) o que dará  84+-0,8428. 

Obs: Os valores z também podem ser encontrados usando a Tabela de Distribuição Normal, enquanto os valores t podem ser encontrados usando a Tabela de Distribuição t. Também estão disponíveis inúmeras ferramentas on-line que podem ser úteis.