Os Derivativos apresentam diversas formas para que o investidor possa criar e utilizar de estratégias de opções para alcançar seus objetivos. E uma das formas mais utilizadas é o modelo de Black & Scholes que é um dos conceitos mais importantes nessa área.
Criado pelos economistas Fischer Black e Myron Scholes – daí vem o nome Black & Scholes – em meados dos anos 70, este é o primeiro modelo amplamente difundido e mais conhecido sobre precificação de opções.
Por isso, é utilizado para calcular o valor teórico usando uma série de variáveis, como preços atuais, preço de exercício, dividendos esperados, taxas de juros projetada, tempo de expiração e volatilidade esperada.
A prática do Black & Scholes
Utilizar na prática este modelo requer muita atenção, pois não é todo valor de opções que pode ser calculado por ele.
Lembra que ao falarmos do Mercado de Opções existem dois tipos delas: as americanas e as européias, esta última que é somente na data de vencimento. Logo, o modelo do Black & Scholes e o modelo Binomial somente funcionaram se utilizarmos o modelo de opções européias, pois essa só pode ser exercido na data do vencimento.
Premissas:
Inclusive, é partindo dessa base de informação que para usarmos o Black & Scholes é preciso compreendermos suas premissas:
- O comportamento do preço da ação corresponde a um modelo lognormal com desvio padrão e média constante;
- Não há custos de transação;
- Os contratos são divisíveis;
- Não há arbitragem possível;
- A negociação de títulos e ações é
- Todos os investidores possuem a mesma taxa livre de risco
- A taxa livre no curto prazo é constante
Assume também:
- O mercado se move de maneira aleatória;
- Movimentos de pequena magnitude muito prováveis e de grande magnitude pouco prováveis;
- Fórmula fácil de planilhar;
- Única variável subjetiva é a volatilidade;
- Largamente aceita no mercado;
- Boa previsão para Hedge.
Como calcular o Black & Scholes?
Para o cálculo desta operação é importante sempre verificarmos suas premissas, pois são a partir delas que a fórmula ganha vida.
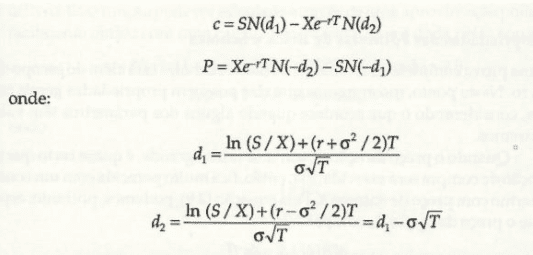
Onde:
- c = preço da opção de compra
- P = preço da opção de venda
- S = preço do ativo
- X = preço de exercício
- r = taxa de juros livre de risco
- ?= tempo para o vencimento
- ? = volatilidade do preço da ação
- N = representa a distribuição normal
Inicialmente pode parecer um cálculo bem difícil, porém não é preciso ser um expert em matemática avançada, mas sim ter um conhecimento matemático que te auxilie no cálculo. Além disso, não é preciso realizá-lo manualmente, hoje existem diversas calculadoras e plataformas que realizam esta equação.
Assim, é utilizando este modelo que será possível chegarmos mais próximo de preços reais futuros de uma opção.
Então, bora aprender mais?
Nós criamos a Trilha de Sucesso para você adquirir o curso para a sua certificação desejada e mais um mix de cursos especiais para você se tornar um profissional Top!
Vem conferir! 😉


Deixe um comentário